By Marshall Chasin, AuD
|
In Part 1 of this article, the acoustic principles of standing waves, damping, and flared tubes were discussed. Part 2 looks at Boyle’s law—both in the more conventional way of transmitting sound through a defined volume or space within the ear canal, as well as what happens in very deep-canal fittings relative to the equivalent volume of the outer ear. |
With the advent of the first truly deep canal hearing aid fitting in the early 1990s (Philips XP peri-tympanic hearing aid), the hearing healthcare field quickly found that less was more. Clinicians were surprised to see how little gain, as measured in a 2cc coupler, was required to generate sufficient amplification for a hard-of-hearing person. In audiological terms, this means that there is a larger real ear-to-coupler difference (RECD). More recently, there have been attempts to revisit the realm of truly deep canal hearing aid fittings.
Mysteries of the Deep Fitting
Strange and wonderful acoustic things can happen with deep canal hearing aid fittings that do not normally present themselves with more conventional shorter canal fittings. Two of them are intimately related to Boyle’s law; one is a direct consequence, and the other is an interesting corollary.
Boyle’s law was developed by Robert Boyle (1627-1691). Boyle was a chemist at Imperial College in London, England, and is considered to be the father of modern chemistry. If you ever get a chance to tour Imperial College, you will see a large plaque on the wall stating that this is where Boyle’s law was discovered. Boyle’s law defines how pressure, temperature, and volume are all interrelated for any given concentration (molarity) of gas.
Boyle’s law states that, as the volume containing a gas decreases, the pressure of the gas increases. That is, they are inversely proportional. Equation 1 shows this relationship:
Equation 1. Boyle’s Law
Pressure ? 1
Volume
Imagine somebody sitting on a balloon. The space that the balloon occupies decreases with the additional weight of a body, thereby increasing the pressure of the air inside the balloon, to a point where the balloon explodes once it can no longer contain the massive pressure built up within its walls.
We can apply this same principle to the mechanics of a deep fitting earmold in an ear canal. The deeper the earmold, the smaller the residual volume between the end of the mold and the tympanic membrane. This decrease in volume causes an increase in generated gain and output (by 4-5 dB) over what might be experienced with a more conventional fitting mold.1
In a conventional hearing aid fitting, the residual volume is on the order of 1.5 cc. With a deep canal fitting, it is approximately 0.5 cc. Each halving of the volume increases the sound pressure by 3 dB. For example, a residual volume of 0.75 cc (half of 1.5 cc) would result in a 3 dB increase, and a 0.37 cc (half of 0.75 cc) volume would result in a 6 dB increase.
This is a well-known (and well used) relationship that every hearing healthcare professional knows, even if they aren’t explicitly aware of Boyle’s law. For instance, we know that we can typically provide additional amplification for clients by providing a new set of earmolds with longer bores, by decreasing the space between the end of the earmold and the tympanic membrane.
But something very interesting can happen for very deep canal hearing aid fittings that is a direct consequence or corollary of this law.
The Ear Drum Is a Brick Wall for Higher Frequencies
To be more accurate, something doesn’t happen for very deep canal hearing aid fittings for low frequency sounds. Figure 1 shows a deeply seated CIC hearing aid, courtesy of Sonic Innovations.
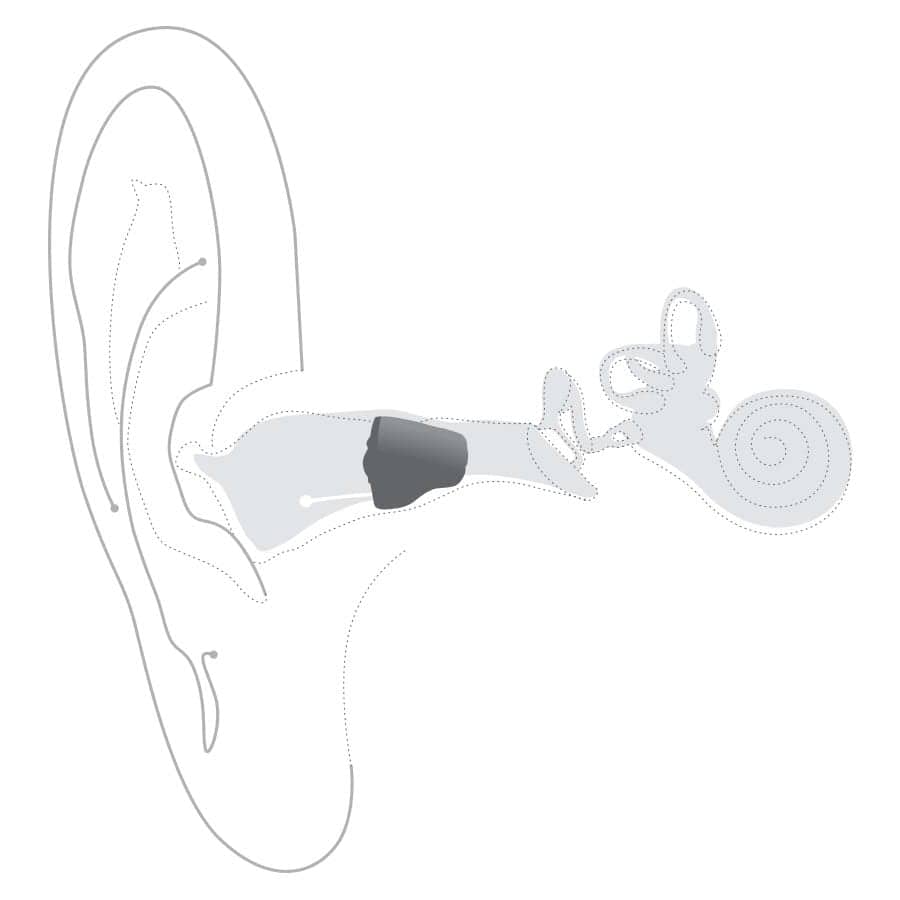
|
| Figure 1. A deeply seated CIC. Photo courtesy of Sonic Innovations. |
It turns out that for deep canal hearing aid fittings, the benefits of Boyle’s law do not apply, at least for low frequency sounds. With Boyle’s law, there is an implicit assumption that the walls of the container are relatively rigid; however, the human ear canal and especially the tympanic membrane, are anything but rigid.
For higher frequency sounds, the ear canal and its tympanic membrane termination do indeed act like a rigid structure; it’s as if the ear canal and tympanic membrane were a brick wall. Figure 2 shows this schematically. For the higher frequency region with deep canal hearing aid fittings, there is indeed a small equivalent volume—the tympanic membrane and the middle-ear ossicles do not contribute to the transduction of sound.

|
| Figure 2. The benefits of Boyle’s law are not as clearly seen for lower frequency sounds. |
Subsequently, the higher frequency sound generation can be precisely predicted based on the actual measured volume between the tip of the deep-seated hearing aid and the tympanic membrane. This is what is meant by the eardrum functions as a brick wall (at least for the higher frequency region).
However, for lower frequency sounds, the volume in front of the hearing aid “appears” to be much larger; it takes into account the residual volume and also the “equivalent volume” of the tympanic membrane and middle ear structures. According to Boyle’s law, a larger (equivalent) volume implies a lower sound pressure level (SPL).
The benefits of Boyle’s law are therefore not as clearly seen for the lower frequency sounds. Boyle’s law contributes up 4-5 dB, but then due to the “larger equivalent volume” phenomenon, about 3 dB of low frequency energy is lost. The net associated benefit in the lower frequencies is only around 1 dB (ie, 4 dB minus 3 dB). Figure 2 shows an artist’s rendition of what low and higher frequency sound energy “see” with a deep canal hearing aid fitting.
Whenever a deep canal hearing aid fitting is considered, the difference between the 2cc coupler response and the real ear response now is affected by the stiffness that is seen in front of the device, but only for the lower frequency region. Larger real ear-to-coupler differences (RECDs) are now observed than with conventional hearing aid fittings. That is, less prescribed coupler gain is required in order to meet the amplification requirements of the hard-of-hearing client.
The Outside End of a Deeply Seated Hearing Aid
In 1974, E.A.G. Shaw while working at the National Research Centre in Canada came up with data that showed that a deep-seated microphone location (on what was to eventually become a deeply seated hearing aid fitting) was optimal for the transduction of higher frequency sound energy. Even though this research was performed almost 40 years ago, current measures are almost identical. And now, unlike the 1970s, we have real-ear measurement systems in our clinics.
|
MORE ON ACOUSTIC PRINCIPLES by Dr Chasin The Acoustics of Hearing Aids, Part 1: Standing Waves, Damping, and Flared Tubes, May 2013 HR. What Your Mother Never Told You About Earmold Acoustic Formulae, November 2009 HR The Case of the Missing C#, June 2012 HR Hearing Aids for Musicians, March 2006 HR CORRESPONDENCE can be addressed to the author at: [email protected]
|
Free amplification from the unobstructed concha and other head and pinna diffraction properties mean that the input sound spectrum is already biased toward the higher frequency region. This is equivalent to saying that, for the higher frequency region, less gain and output need to be prescribed in order to obtain optimal amplification for a hard-of-hearing client than if they were fit with more conventional amplification where the microphone was situated further from the ear canal entrance.
Specifically, the concha resonance, which is around 4000-5000 Hz, adds 5 dB to 8 dB of additional gain2 even before the sound reaches the deeply seated hearing aid. Since this is something found in the real ear, but not a 2cc coupler, the real ear-to-coupler difference is even greater for deep ear canal hearing aid fittings.
Table 1 shows a summary of these effects that would be found in a deep canal hearing aid fitting over a more conventional hearing aid for the lower frequencies (250-500 Hz), the mid frequencies (1000-2000 Hz), and the higher frequencies (2000 Hz +). For example, in the higher frequency region, 8 dB less gain and output are required than in more conventional hearing aid fittings in order to achieve any desired fitting target for your client.
Summary of Free Acoustical Benefits for Deep-canal Hearing Aid Fittings
- Due to Boyle’s law, there is 4 dB of free amplification across all frequencies.
- Optimal microphone location in the ear canal provides an additional 3-4 dB of high frequency gain and output above 2000 Hz.
- Having a compliant tympanic membrane and middle ear system means that for the lower frequency sounds, a larger equivalent volume is seen and the benefits of Boyle’s law are minimized with a net benefit of only a 1 dB improvement.
This all results is less gain having to be prescribed, especially in the higher frequency region, with more significant high frequency hearing losses being able to be fit.

|
Marshall Chasin, AuD, is the director of auditory research at the Musicians’ Clinics of Canada in Toronto and the coordinator of research at the Canadian Hearing Society. He is also an associate professor in the School of Communication Sciences & Disorders at Western University, and adjunct professor at the University of Toronto (in Linguistics) specializing in Acoustic Phonetics. |
References
1. Cox RM. Acoustic aspects of hearing aid-ear canal coupling systems. Monographs in Contemporary Audiol. 1979;1(3):1-44.
2. Yost WA, Nielsen DW. Fundamentals of Hearing: An Introduction. 2nd ed. New York: Holt, Rinehart and Winston; 1985.






