Relating musical principles to audiological principles
You say “440 Hz” and musicians say “an A note”; you say “105 dBSPL” and musicians say “fortissimo.” (Let’s call the whole thing off!) Most of the underlying physical properties that give musical instruments their unique tonal characteristics are also the same physical properties we take advantage of during the fitting of BTEs and other hearing instruments.
Without explicitly recognizing it, audiologists and dispensing professionals have all of the tools for the understanding and analysis of music. In some cases any limitation can be traced to lack of application of a concept and in other cases it is merely terminology. The musical notes versus the frequency in Hz is one such area.

FIGURE 1. Several notes shown on a treble clef along with their frequencies. (Figures in this article from Musicians and the Prevention of Hearing Loss, 1st edition by Chasin, 1996. Reprinted with permission of Delmar Learning, a division of Thomson Learning.)
Letters and Frequencies
Musicians use the letters A, Bb, C, whereas hearing care professionals would say 440 Hz, 466 Hz, and 524 Hz. According to the situation and information required in both cases, this may tend to be an oversimplification. Depending on the musical instrument, the note A may have a fundamental (or tonic) on A, but also a range of higher frequency harmonics and overtones with location and intensities defining the musical instrument.
Similarly, stating that a certain note (or vowel) is sung at 440 Hz ignores the fact that there is a rich harmonic structure that occurs at the higher frequencies. Accepting this limitation, a notation that has received widespread acceptance is to state the note as A[440Hz] or more simply as A[440]. This means that the A on the second space of the treble clef (Figure 1) has a frequency of its fundamental of 440 Hz. Other notes and frequencies are shown in Figure 1.
A convenience of the musical letter terminology is that octaves have the same letter notation: an octave higher than A is A. And a convenience of the frequency notation is that a doubling of the frequency number is one octave higher; 880 Hz is one octave above 440 Hz. Clearly the frequency notation can be more accurate, but within any one cultural style of playing, the letter terminology can be more than sufficient and more innately understood.
Letters and Intensities
Another notational difference between music and audiology is the specification of loudness and the actual intensity range. Musicians speak in terms of a note being “pianissimo” or “forte,” whereas an audiologist might refer to the level of intensity of a note as being 45 dBSPL or 105 dBSPL. Both are correct despite the slightly more accurate use of the decibel measure for the intensity of the sound.
Of course, the reference to a note being “pianissimo” or “pp” refers to the loudness and not the intensity, but given this difference and the limitations of comparison of a perceptual and a physical measurement, the usage can still be fairly accurate. Musicians around the world can easily play a passage denoted as “mezzo forte” or “mf” with similar intensities because of an underlying familiarity with what the perceived intensity should be. Table 1 shows the approximate relationship over a number of musical instruments and styles for a stated loudness level and its corresponding intensity range.
Acoustic Resonance and Musical/Hearing Instruments
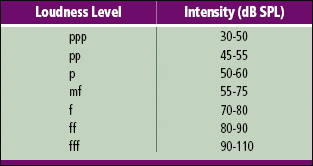
TABLE 1. The approximate relationship between a musician’s loudness judgement and the physical intensity measured in decibels (SPL). (Tables in this article from Musicians and the Prevention of Hearing Loss, 1st edition by Chasin, 1996. Reprinted with permission of Delmar Learning, a division of Thomson Learning.)

TABLE 2. Examples of musical instruments that behave primarily as either a quarter-wavelength or a half-wavelength resonator.
Like all tubes and chambers, musical instruments behave acoustically as resonators. Resonators are structures (eg, tubes) that serve to amplify sounds that are near the characteristic or resonant frequency. In some cases the resonant frequency of the tube can be changed either by physically elongating it (eg, trombone) or by covering holes (eg, clarinet). And, similar to the human vocal tract, these resonators can be classified as quarter-wavelength, half-wavelength, and Helmholtz resonators. Table 2 lists some musical instruments that are considered quarter-wavelength and half-wavelength resonators.
Quarter-wavelength resonators.
A quarter-wavelength resonance occurs whenever a tube has one “open” end and one “closed” end. These occur often and are typically first studied at the high school level. If you pinch a straw at the bottom and blow across the top of the straw, a unique frequency is heard that is governed only by the length of the straw. If you had strong enough lungs, blowing harder would elicit an additional frequency at exactly three times the frequency of the previous one.
This is one important feature of a quarter-wavelength resonator: successive resonances are at odd-numbered multiples of the resonant frequency. So, no matter what the tonic note is in this type of resonator, other harmonics can be heard.
We also see this in behind-the-ear (BTE) hearing aid acoustics: the hearing aid receiver tubing + earhook + earmold tubing length combines to generate a resonance at about 1000 Hz. Because the hearing aid is “closed” at the receiver end and “open” at the end of the earmold, this functions as a quarter-wavelength resonator. There are successive “tubing-related” resonances at 3000 Hz and 5000 Hz—the odd-numbered multiples of 1000 Hz. In a BTE hearing aid electroacoustic response, there are also resonances in between these wavelength resonances and these are related to the mechanical properties of the hearing aid receiver. Prior to the mid-1980s, hearing aids typically used either Class A or Class B output stages with a mechanical receiver-related resonance at 2000 Hz. However, since the advent of the Class D output stage, most receivers possess a 2700-3000 Hz resonance and may be coincidental with the second mode of the tubing-related resonance at 3000 Hz.
The formula for a quarter-wavelength resonator is given by:
F = (2k-1)v/4L
Where,
F = Frequency (Hz)
v = Speed of sound
L = Length of the tube
k = Mode or resonance number

FIGURE 2. The length (L) of the clarinet is from the mouthpiece down to the first non-covered hole (black dots mark covered holes). The region below the first non-covered hole (shaded in light gray) does not contribute to the pitch. (From Musicians and the Prevention of Hearing Loss, 1st edition by Chasin, 1996. Reprinted with permission of Delmar Learning, division of Thomson Learning).
The term (2k-1) is merely a convenience to show that the resonant frequency F not only occurs at v/4L but also at 3v/4L and 5v/4L. Specifically, if k=1 (the first mode of the resonance), then the term (2k-1) is simply equal to 1. But, if k=2 (the second mode of resonance), then the term (2k-1) equals 3, and so on.
This formula is also used in speech acoustics and explains why for the vowel [a] as in “father”—where the mouth is “closed” at the vocal cords and “open” at the open lips—the resonant pattern of [a] has odd numbered multiples of the primary resonance 500 Hz. The 500 Hz can be calculated from the above formula and is based on the length of the human vocal tract (about 17 cm). Subsequent vocal tract resonances (also called formants) are at 1500 Hz (3 x 500 Hz), 2500 Hz (5 x 500 Hz), and so on.
Getting back to musical instruments, clarinets and brass instruments have odd-numbered multiples of their fundamental frequency because they are “closed” at the lips and “open” at the other end, causing them to behave primarily as quarter-wavelength resonators. Other than the fundamental (eg, A[440]), there are inherent resonances from these instruments at 1320 Hz (ie, 3 x 440 Hz) and 2200 Hz (ie, 5 x 440 Hz). Figure 2 shows that the “length” of the clarinet is from the mouthpiece down to the first non-covered hole. The length below the non-covered hole does not contribute to the acoustics of the instrument.
One aspect of having odd-numbered multiples of the fundamental or primary resonance is that, in each octave, there is less energy than if there were resonances at integer numbers of the fundamental (eg, violin). The harmonic structure is less dense for a quarter-wavelength resonator than for a half-wavelength resonator. Another aspect of a quarter-wavelength resonator is that they have a “register key” and not an “octave key.” In the clarinet, the register key increases the frequency of the note by three times the fundamental, which is in line with the expectation of all quarter-wavelength resonators. When one plays middle C (concert) on a clarinet, the note is 262 Hz, and when the register key is depressed, the note changes to high G[784], which is almost exactly 3 x 262 Hz. Essentially, G[784] is one and one-half octaves above concert C[262].
Half-wavelength resonators
Unlike the quarter-wavelength resonators that require a “closed” end and an “open” end, half-wavelength resonators occur in tubes that are either “closed” at both ends or “open” at both ends. Flutes and piccolos function as half-wavelength resonators that are “open” at both ends, and violins and guitars function as half-wavelength resonators that are “closed” at both ends. In the stringed instrument category, it is the string that is held rigidly at both ends.
The formula for a half-wavelength resonator is given by:
F = kv/2L
Where again:
F = Frequency (Hz)
v = Speed of sound
L = Length of the tube
k = Mode or resonance number.
In this formula, the higher frequency harmonics are merely integer multiples of the primary or fundamental frequency or the tonic. In a half-wavelength resonator instrument, such as the flute or violin, the first resonance above concert C[262] would be one octave higher at C[524]. The next would be an octave higher again at C[786], and so on, but always remaining the tonic. Half-wavelength resonator instruments can have “octave keys”—keys that increase the frequency by exactly one octave (a doubling of frequency). Figure 3 shows the clarinet (a quarter-wavelength instrument) and a flute (a half-wavelength instrument) playing the same concert note (G[392]), and normalized for playing-intensity, demonstrating the differing resonant structures.

FIGURE 3. The clarinet (a quarter-wavelength instrument) and a flute (a half-wavelength instrument) playing the same concert note (G[392]), and normalized for playing-intensity, demonstrating the differing resonant structures. The flute has twice as many resonances in any given frequency range as does the quarter-wavelength resonator clarinet.
Flaring Tubes: Conical Instruments Act Like Half-Wavelength Resonators
For reasons beyond the scope of this article, it turns out that conical or gradually flaring tube instruments also behave as half-wavelength instruments. The oboe and saxophone are “closed” at the mouthpiece end and “open” at the other end, but because of their natural conical flare of the tube, they behave acoustically as if they are half-wavelength resonator instruments. Both the oboe and the saxophone have an “octave key” that serves to double the frequency of playing.
An aspect of all half-wavelength resonator instruments is that the harmonic structure is denser than that of an equivalently sized quarter-wavelength instrument. Within each octave, there are two points of energy (at the octaves) whereas for quarter-wavelength instruments there is only one (or stated differently, two points of resonant energy every octave and one half).
The key point here is that stringed instruments, as well as the saxophone and oboe, act like half-wavelength resonators and produce sound in whole-number multiples of their fundamental frequency.
Volume-Related and Mechanical Resonances
Other than the two wavelength-related resonances (quarter and half)—whose behavior can be ascertained from the end (or boundary) conditions of the tube and the length of the tube—there are resonances that are derived from the volume of air or mechanical characteristics of the wood of the instrument. These non-wavelength resonances are primarily found below 2000 Hz but can be seen as small magnitude ones in the higher frequencies.
For example, suppose you strike a tuning fork on your knee and then turn around and place it on the blackboard. While in contact with the blackboard, the tuning fork is much louder; we are driving the natural resonance of the blackboard, which is in the frequency region of the tuning fork sound. This natural resonance has to do with the size of the board and the material that it is made of.
Musical instruments understandably have these volume or material-related resonances that serve to enhance the intensity of certain frequencies within the amplifying range of the resonance. A flute has a mechanical natural resonance at 880 Hz (which is coincidentally an A) and it is very difficult to play this note quietly. Musicians would refer to this as the “fat” part of their instrument. With training and skill, they can learn to harness this natural resonance and shape their musical selections with well-controlled intensity dynamics.
Percussive Instruments
Percussive instruments generate sounds by incurring a sudden hit on a structure or string. The result can be very tonal or atonal depending on the nature, composition, and shape of the instrument being hit. A characteristic of all percussive instruments is that the resulting sound is broadband in nature and has significant energy in the higher frequencies.
In these cases, it is best to consider the case of a waveform in the time domain. When a percussive instrument is hit, there is a “sudden” change in pressure to a much higher one in a short period of time. If you think about this in terms of the resulting wavelength, this first quarter of the wavelength (from quiet to an intense level), being very sudden, is also very short temporally. Therefore, the entire wavelength would be short as well indicating a high-frequency sound. You cannot have a low-frequency sudden sound. That is why all sounds in languages of the world that have plosives (eg, aspiration, affricates, clicks, and pops) are high-frequency.
This of course does not mean that all of the sound of that percussive instrument is high-frequency. A bass drum has a significant amount of high-frequency energy because it is hit suddenly, but also has a significant amount of low-frequency energy because of the large surface area of the drum head and large volume of trapped air that possesses a low-frequency resonance. But the point is that percussion has significant high-frequency sound energy.
Summary
Musicians use the notes ranging from A to G along with sharps and flats, and hearing care professionals use frequencies measured in Hz. A convenient notation is a combination of the two—for example, A[440] meaning that the fundamental (or tonic) of the note “A” is at 440 Hz.
The nature of the higher frequency harmonic structure resulting from the played fundamental note will depend on the acoustic characteristics of the instrument. Instruments that are tube-like and are “closed” at the mouthpiece and “open” at the other end are considered to be quarter-wavelength resonators and as such will have additional higher frequency resonances at odd numbered multiples of the fundamental. The first additional higher frequency resonance of these instruments would be at 3 times (an octave and one half) the frequency of the fundamental. Examples of these instruments are the clarinet and the brass instruments.
Instruments that are either “closed” at both ends (eg, stringed instruments) or “open” at both ends (eg, flute) are considered half-wavelength resonators and will have higher frequency resonances at integer multiples of the fundamental. The first additional resonance with these instruments will be one octave higher than the fundamental.
Half-wavelength resonator instruments can have an “octave” key, whereas quarter-wavelength resonator instruments can have a “register” key (one and one half octaves).
Some instruments that are “closed” at one end and “open” at the other still behave like half-wavelength resonators, and these are those instruments that have a conical flare such as the oboe and the saxophone. The nature of the material, and the shape and size of the instrument, may also yield frequency regions that enhance the intensity of the sound. In the flute, this region is at 880 Hz and is called the “fat” region.
Acknowledgement
This article was adapted with permission from the chapter “Music for the Audiologist” that appears in Dr Chasin’s book Hearing Loss in Musicians (pages 129-136). Copyright©2009 Plural Publishing Inc. Reprinted with permission. All rights reserved. For more information or to purchase the book, visit www.pluralpublishing.com.
Correspondence can be addressed to HR or Marshall Chasin, AuD, at .
Citation for this article:
Chasin M, Hayes D. Music for the hearing care professional. Hearing Review. 2010;20-25.





