A review of the key physical principles of power as they relate to acoustics

|

|
| Christopher Schweitzer, PhD, is an audiologist and president of HEAR 4U International, Lafayette, Colo, as well as serving advisory roles in Audigy Group and Able Planet. Desmond A. Smith is a research scientist for Acoustimed (Pty) Ltd, Johannesburg, South Africa. | |
The daily activities of hearing care professionals have lineal connections to the foundational investigators of the productive management of power, energy, and electricity. These connections are often lost or obscured in the twittering speeds of the digital age. But in a very real sense, every measured hearing loss and every delivered hearing aid carries with it traces of the “thought work” of curious innovators from prior centuries.
This two-part article briefly traces some of the historical contributions of just a few luminaries of that ancestral legacy. We’ll attempt to render it in such a way as to create a novel context for readers to think differently about power, loudness, and the repackaging of sound for auditory augmentation via hearing aids. Part 1 focuses on portions of that pertinent, but sometimes peculiar, history that relates to amplification. Part 2 looks more specifically at the relation of loudness to power. It will also include a discussion of how a review of this history and a synthesis of its relevant properties have led to a new approach to audio amplification that may serve a valuable protective function for users of audio electronic devices, including hearing aids.
Giants in Our Family

|
| FIGURE 1. Alexander Bell, 1847-1922. |
In testing hearing thresholds in units of dB, most hearing care professionals know that the scale is in honor of Alexander Graham Bell (Figure 1) to whose name is appended the “deci” for refinements of that scale. Many also know that Bell’s wife, Mabel, had profound hearing loss, as did his mother. Bell was dedicated to amplifying the transmission of the human voice with hopes of penetrating the obstacles that they and others confronted in spoken communication. The relatively new science of applied electricity loomed as a likely candidate to pursue that goal. Hence, an abiding interest in overcoming the barriers of hearing loss was intimately connected to the birth of the vast telecommunications networks that currently serve the entire planet from satellite TV to texting and Twitter.
The “bel” was originally called the TU, or transmission unit. It was devised by engineers of the Bell Telephone Laboratories to quantify losses in signal level over a 1-mile length of telephone cable. The bel was inconveniently large, hence, a reduction by a factor of 10. The decibel became the more common usage, as attested by the ubiquitous “dB” that spreads across most activities of hearing care professionals. It would be remiss to neglect to mention also that enormous contributions to the foundational development of audiometry, electronic hearing aids, and the science of psychoacoustics were spearheaded by Harvey Fletcher and his colleagues at what was to become the Bell Laboratories.
But as frequently as hearing professionals work with well-calibrated sound generators and psychophysical charts that tag sensitivities in dB, it may surprise the reader to learn that there is a perhaps peculiar, but clear, connection between horses and hearing aids, horsepower and “hearpower.” For that, a longer step back in time is required.
Watt’s Seminal Computations

|
| FIGURE 2. James Watt, 1736-1819. |
Considered the first practical engineer, the Scottish inventor James Watt (Figure 2) is best known as the enabler of the Industrial Revolution—the man who perfected the mighty steam engine. His motivation, of course, was to develop more efficient “work” and the result was considerable wealth. The work accomplished by a 21st-century hearing aid has a convoluted, but genuine, ancestral relationship to Watt. It’s the work component here that will tie the patient reader forward into the realm of hearing science and amplification.
The essence of the Industrial Revolution was the implementation of machines to replace the direct efforts of poorly muscled humans and well-muscled, but not so savvy, horses. James Watt made extensive studies of the work and power properties of horses (and ponies) tethered to mill wheels and other devices, mostly in mines and breweries. When a horse raised 550 pounds of weight a distance of 1 foot, they did work (imparted energy) of 550 foot-pounds. Horses were a necessarily large component in manufacturing operations in the 1700s. But, theoretically, by means of a well-designed system of pulleys, a mouse could also add 550 foot-pounds of energy to a bucket of coal. The difference is that a horse can exert a bigger force and do the job in 1 second versus some considerably longer time for the mouse. Hence, HorsePower is understandably greater than MousePower in head-to-head competition. This also makes it clear that time is a component in the analysis of work—a pertinent point as the story leads toward Hearpower.
By some accounts, Watt determined that a horse could turn a mill wheel 144 times in an hour (or 2.4 times a minute). The wheel was 12 feet in radius, therefore the horse traveled 2.4 × 2p × 12 feet in 1 minute. Watt judged that the horse could pull with a force of 180 pounds (assuming that the measurements of mass were equivalent to measurements of force in pounds-force, which were not well-defined units at the time). Again, it’s important to note the component of time in this equation.
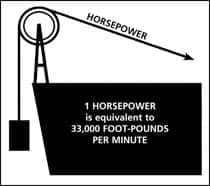
|
| FIGURE 3. Computation of horsepower: 1 Horsepower = 550 pounds raised 1 foot in 1 second = 76.04 kg raised 1 meter in 1 second. Note that 550 pounds raised 1 foot represents an amount of stored energy (or work done) while the power is determined by how quickly the energy can be stored. The rate at which energy is stored is determined by both force and velocity (power is calculated as the product of force and velocity). |
Watt’s careful observations and notes at the onset of the scientific mechanization of industry led to the general replacement of the term “horsepower” with units of power named, of course, after Mr Watt. And it is power in the human auditory experience that is the focus of this tutorial, so a general appreciation of watts, kW, mW, and µW is useful.
If an electrical machine could run at 100% efficiency (not a possibility) and produce 746 watts of power, it would be rated as having 1 electrical horsepower (Figure 3). Power in watts relates to a rate of energy conversion. Some additional examples might place things into perspective. A solar collector on a housetop generates around 4000 watts of electricity; a cruising automobile produces about 25,000 watts (25 kW) of mechanical energy (33.5 horsepower); the computerized monitor on an exercise machine at a gym might inform the sweating jogger that they are working at a rate of 200 watts.
A jiggling of the eardrum at 1000 times per second at a power level of 10-16 watts/cm2 will enable someone with good hearing to perceive a soft tone. A 130 dB increase of that jiggling will lift the sensation of that tone up to a painful experience. This amounts to an astonishing 3 trillion times power increase to 0.0003 watts/cm2!
For perspective, a common laser pointer might have five one-thousandths of a watt (5 mW) of power, and the power of a hearing aid is likely to be on the order of several hundred millionths of a watt (µW). However, some hearing aid operating specifications, such as battery drain, are more typically expressed in terms of the current milliamp hour (eg, 2 mA). So another historic name warrants mention at this point.
The Need to “Amp”lify

|
| FIGURE 4. Andre Marie Ampere, 1735-1836 |
Andre Marie Ampere (Figure 4) worked in France in the late 1700s and early 1800s researching the relationship between magnetism and electricity. While the terms have changed and the science has obviously evolved, Ampere laid the foundation for “electrodynamics” upon which every audiometer and hearing aid operates. The ampere (amp) is a measure of the amount of electric charge that passes a given point per unit time. Approximately 6.242 × 1018 electrons passing a fixed point each second constitutes one ampere. But let’s step back to the 18th century for a moment before building that hearing aid, and examine some additional physical properties that relate to the “work” done by a hearing aid.
In a time before bowling alleys, many “thought experiments” involved the dynamics of weaponry. So, imagine a 1 kilogram cannon ball lifted up to a height of 1 meter. Because of its new height, the cannon ball has acquired additional energy, namely, 1 meter-kg. Working against gravity, it presses downwards on a surface with a force (weight) of 1 kg. When the ball is released or is rolled down a slope, it naturally accelerates. When it reaches the bottom of the slope, it will have acquired kinetic energy, which would keep it moving downward or rolling in a horizontal direction at a speed in accordance with an object’s acceleration due to gravity (9.8 meters per second per second). That is equivalent to the potential energy that it had while working against gravity from a height of 1 meter above the horizontal surface.
The principles of electronics, around which hearing devices are designed, indicate that one can charge a capacitor with a voltage that represents a discrete number of electrons—or a “quantum” of potential energy. If the capacitor is discharged through a resistor, the resistor heats up and the electrons whiz about with newly acquired kinetic energy. This is the same quantum of energy, but in a different form. The total amount of energy is either in the voltage or in the heat, or at some stage possibly in both. Hence, to calculate the total energy in the system, one must add the voltage (force) to the calories (heat). The current that flows through the resistor only while the capacitor is discharging is analagous to the acceleration of the cannon ball while it, too, was changing states from potential to kinetic energy (Figure 5).
Thank You, Alessandro Volta: “Wearable Work” Requires Batteries
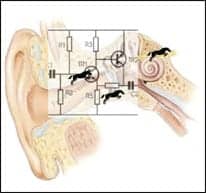
|
| FIGURE 5. A hearing aid’s amplifier circuit supplies nano levels of horsepower to increase the energy available to a structurally weakened hearing system. |
Honored as a count by Napoleon, Alessandro Volta (Figure 6) was a northern Italian contemporary of Ampere. Volta made numerous crucial advancements in electric cell design and fabrication. Had it not been for Volta’s studied determination, otoscopic exams might be conducted by candlelight and hearing aids would consist of battery-less Helmholtz resonators.
The “work” in a battery is applied to charged particles at the chemical (ionic) level of the contents of the battery cell. Voltages relate to differences between charged particles, but for simplistic purposes it’s fair to say that the 1.2 V battery gets its rating according to rules that Count Volta helped devise. These rules relate “power” directly to the heat and electromotive force that yields the potential work-per-second those particles can exert. Since all of this “potential” work and heat seem rather messy, it needs a good sheriff in town to lay down the law. So, let’s hire one from Bavaria.
A Brief History of Ohm and Ohm’s Law
The universe began, according to some versions of Hindu creation stories, by sound. In one version, the spreading hum from the void at Vishnu’s awakening and the birth of Brahma—OM—penetrates all, and still perpetuates within the subatomic quantum vibrations. But the Ohm that electronic amplifier designers hold dear has a more recent and less meditative history.
Georg Simon Ohm (Figure 7) was a German high school teacher born in 1787 in Erlangen, Bavaria (which is, incidentally, the location of the world headquarters of Siemens Hearing Instruments). Ohm started his research with the electric cell recently invented by Count Volta. But Ohm used equipment of his own creation to determine that the current flowing through a wire is proportional to the wire’s cross-sectional area and inversely proportional to its length.

|
| FIGURE 6. Count Alessandro Antonio Anastasio Volta, 1745-1827. |
Based on his experimental work, Ohm defined the relationship between voltage, current, and resistance still fundamental in electronic design and applications. These relationships are of such great importance that they represent the true beginning of electrical circuit analysis. Like many of history’s “advance scouts,” Ohm was ridiculed and his findings rejected by establishment colleagues when he published them in 1827. In fact, he was forced to resign from his teaching position and became impoverished. Fortunately, his work gained support outside of Germany, and in 1849 Ohm was finally recognized for his contributions with an appointment at the University of Munich.
Ohm’s law states that power is calculated by multiplying the voltage by the current. It assumes an infinite amount of energy keeping the voltage constant so that there is a constant acceleration of electrons. This is equivalent to a cannon ball rolling down an infinitely long slope. Hence, Ohm’s law might be seen as relating to a battery with a finite amount of chemical energy stored in it. In the case of a battery, the energy converted to heat is exactly the same as the energy originally stored in the battery. It is certainly true that a fresh battery can exert a greater force and therefore exert more power than a flat battery, but in the end, the amount of work done depends on the capacity of the battery. Ohm’s law is expressed as:
V = I x R
… where V is the applied voltage, R is the resistance in ohms, and I is the current in amperes.

|
| FIGURE 7. Georg Simon Ohm, 1787-1854. |
Ohm’s law demonstrates that, if the applied voltage across a circuit is increased or decreased, the current generated in the circuit increases and decreases, respectively. Furthermore, as the resistance in a circuit increases, the current generated in the circuit decreases. Using one of three algebraic variations of Ohm’s law, and any two known variables, one can solve for the other unknown quantity:
I = V / R
R = V / I, so …
Power (in watts) = V x I
And Still One More 19th-Century Giant
The son of an English brewer, James Joule (Figure 8) made crucial contributions to the practical use of electrical power and its relation to heat. The international standard unit (SI) of energy, the joule, is named after him.
The industrious and mostly self-taught Joule worked with Lord Kelvin in developing the absolute scale of temperature, and he made numerous observations on electromagnetic behavior. He also determined the relationship between electrical current moving through resistance and the heat dissipated in the process in what is now known as Joule’s law. However, it could also be said that considerable confusion between force, power, work, and energy may have originated with Joule’s own misuse of these terms (see sidebar). Those who repeated and refined his measurements were too polite or respectful to question that his power calculations were applied to the relationship of work and heat, which are both quantities of energy, not power. Nevertheless, Joule unquestionably also has an ancestral hand in the design and operation of 21st-century hearing aids.
And Back to Hearing Again
How does this predigital history apply to the routine daily work of hearing professionals? The entire endeavor of amplification is a matter of repackaging clumps of energy. From the vast range of vibratory events that may arrive at the head of an individual with hearing impairment, the professional applies amplifying “machines” to increase the power of “meaningful” molecular patterns, which might otherwise be inaudible to perceivable sensation levels. Simultaneously, energetic packets that are already sufficiently loud need treatments and controls to prevent excesses to the listener.
The perception of loudness is essentially derived from the amount of energy supplied at the auditory input (ie, the eardrum). However, the hearing system also has a unique “time window” mechanism that, among other things, avoids energy accumulating ad infinitum to a condition of infinite loudness. This is done by dumping energy from sounds with durations longer than approximately 100 milliseconds.1 For shorter times, the loudness is directly equivalent to the duration of the sound.
Hearing professionals commonly commute between the two dimensions of intensity and frequency. Hence, the vital third dimension of time is often obscured or forgotten.2 Very brief sounds of less than 5 milliseconds may require as much as 20 dB more intensity to be audible. This has an assortment of auditory consequences that will be addressed in Part 2, along with a discussion of how these principles relate to everyday perception of loudness.
Conclusion
This brief discussion provided a review of the fundamental history and several often-confusing principles of mechanical and electrical power, force, and energy, and their relation to audition and amplification. In Part 2, we will delve further into the relation of these physical principles to everyday loudness perception. We will also discuss how an understanding of these premises relates to a new amplification approach that exploits properties of psycho-acoustics and permits a protective approach to sound processing.
References
- Zwislocki JJ. Temporal summation of loudness: an analysis. J Acoust Soc Am. 1969;40(2):430-441.
- Schweitzer C. Time: the third dimension of hearing aid performance. Hear Instr. 1986;37(1).
- Joule JP. On the Changes of Temperature Produced by the Rarefaction and Condensation of Air. Philosophical Magazine. 1845; Series 3;26: 369. Available at: books.google.com/books~.
Correspondence can be addressed to H. Christopher Schweitzer, PhD, HEAR 4U International, 2505 Ginny Way, Lafayette, CO 80026; e-mail: , or Desmond A. Smith at .
Citation for this article:
Schweitzer C, Smith DA. From horsepower to hearpower. Hearing Review. 2009;16(7):10-15.
Correcting Mr Joule

|
| FIGURE 8. James Prescott Joule, 1818-1889 |
Measurements by Joule led him to estimate the mechanical equivalent of heat as 838 foot-pounds of work to raise the temperature of a pound of water by 1° F. Notice that the reference is to the unit of “work” (energy measured in foot-pounds) required to raise the temperature of a pound of water 1° F. However, in his 1845 paper,3 Joule wrote:
“… the mechanical power exerted in turning a magneto-electric machine is converted into the heat evolved by the passage of the currents of induction through its coils; and, on the other hand, that the motive power of the electro-magnetic engine is obtained at the expense of the heat due to the chemical reactions of the battery by which it is worked.” [italics added]
The passage should be read as:
“… the mechanical energy expended in turning a magneto-electric machine is converted into the heat evolved by the passage of the currents of induction through its coils; and, on the other hand, that the motive force of the electro-magnetic engine is obtained at the expense of the heat due to the chemical reactions of the battery by which it is worked.”





